博弈论:混合策略
纯策略:玩家在博弈中采用确定性的、不带有随机性的策略。简而言之,玩家通过选择一个特定的行动或策略来参与博弈,而且这个选择是确定的,没有随机性。
混合策略:玩家以一定的概率分布选择纯策略。在这种情况下,玩家不是坚持采用一个确定的策略,而是以一定的概率分布来随机选择不同的纯策略。混合策略可以用概率分布来表示,其中每个纯策略都有相应的概率。
上面给出了之前提到的纯策略和这次讲的混合策略的定义。我们可以用公式来表达这两者:
纯策略:$A_i = {a_{i1}, a_{i2}, \dots, a_{i n_i}}$,其中纯策略$a_{i}\in A_{i}$。
混合策略:给每个纯策略一个概率分布。用$\Delta \left(\mathcal{A}_{i}\right)$表示$A_i$上的概率分布,即:
则混合策略$p_i \in \Delta A$。
期望收益:在随机策略中,要计算期望收益,那就需要纯策略的博弈结果的收益乘上这个结果出现的概率,对每个博弈结果进行求和,这个应该比较好理解。
混合策略的目的:不论你使用哪一种行动,对方的收益都不变。这句话体现了混合策略的意义:
- 增加不确定性和避免可预测性: 混合策略允许玩家以一定的概率分布随机选择不同的纯策略。通过引入随机性,混合策略使得其他玩家很难准确预测某个玩家将采取的确切行动,从而增加了对手的不确定性。并且玩家能够在一定程度上避免被对手轻松预测,因为他们无法确定下一步会选择哪个具体的纯策略。
不过,这也为自身收益带来了不确定性:混合策略的本质是通过一定的概率分布随机选择纯策略,因此每次实施混合策略都可能导致不同的结果。
尽管混合策略增加了不确定性,但混合策略纳什均衡的定义确保了玩家在采用混合策略时仍能够取得最优收益。在混合策略纳什均衡中,玩家的混合策略是其他玩家采用混合策略的最佳响应,因此玩家不能通过单方面改变自己的概率分布来提高自己的效用。
求解混合策略纳什均衡
根据纳什定理,有限的策略式博弈一定存在混合策略纳什均衡。因此,给定不同策略的期望的情况下,是可以求得纳什均衡的概率的。
例如:
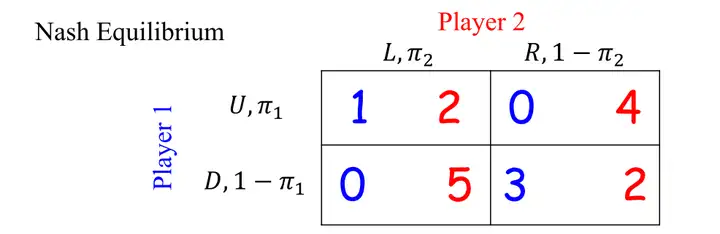
上面的例子中,玩家1有$\pi_1$的概率选择$U$,玩家2有$\pi_2$的概率选择$L$。那么,我们只要令两者的期望收益相等,就可以求得这两个概率。
由玩家2选L的期望收益等于玩家2选R的期望收益,可以得到:
$2\pi_1+5(1-\pi_1)=4\pi_1+2(1-\pi_1)$,解得$\pi_1=0.6$。
由玩家1选U的期望收益等于玩家1选D的期望收益,可以得到:
$\pi_2=3(1-\pi_2)$,解得$\pi_2=0.75$。
因此纳什均衡是
只要记住,当选择混合策略时,玩家的不同策略的期望收益应该相同,就可以轻松求得纳什均衡的概率。
上面这句话可以这么理解,假如玩家的不同策略的期望收益不同,那么玩家就会选择高收益的策略,这就又回到了纯策略了。
hexo写Latex太难写了,就这么短短几个字搞了快两小时都没好。
2024/1/14 于苏州