生成式推荐：RQ-VAE

最近开始接触一些生成式推荐的范式，实际上也是赶了个晚集了，早在2023年，生成式模型就进入了推荐算法工业界的视野，以谷歌Tiger为主的一系列框架在随后两年发展迅速，今年国内的大厂也纷纷落地。接着这个周末，学习一下其中较为核心的RQ-VAE。

从Item ID到语义ID

在推荐算法发展到Embedding+DNN的范式之后，整个行业的特征相对规范化，尤其是电商行业里，底层特征大多数是由Item ID，User ID，画像特征，行为序列组成。其中的Item ID，通常是item经过hash编码得到的一个独立ID，然后通过查表获取Embedding。这已经足够好用，不过依然会面临几个问题：

Hash碰撞
采用原始的物品 ID将导致词汇表非常大
数字ID处理冷启动表现不佳
无法利用item自身语义

因此，学术界提出了语义ID（Semantic ID），用多个ID来表示一个item。而实现它的方式就是RQ-VAE。要了解它，需要先了解一下VAE。

VAE

RQ-VAE是对VAE（自分编码器）的改进，后者是一个生成模型，目标是通过学习输入数据的分布，输出类似的分布，使用KL散度作为评估指标。

VAE的结构由编码器，重参数化和解码器组成：

编码器将输入映射为描述隐变量$z$的两个分布参数，即两个向量：均值 $\mu(x)$ 和标准差 $\sigma(x)$。
学习潜在分布时涉及随机采样，而采样这一操作不是可微分的，导致梯度无法回传，因此需要重参数化把采样过程可微化：
$$
z = \mu(x) + \sigma(x) \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, 1)
$$
最后解码器将潜在变量 $z$ 转换回数据空间，得到重构的 $\hat{x}$，也就是模型学习的原数据分布。

VAE 的损失由两部分组成，其中重构损失保证重建数据与原数据相似。KL散度让潜在空间接近标准正态分布，便于采样生成新数据。
$$
\mathcal{L} = \underbrace{\text{重构损失} ; | x - \hat{x} |^2}{\text{确保数据重构准确}} +
\underbrace{\text{KL散度} ; D{KL}(q(z|x) | p(z))}_{\text{约束潜在变量分布}}
$$

VAE应用的范围比较广，生成式模型，信息压缩都有用到，这篇文章仅提及其信息压缩的应用。

VAE的信息压缩

简单来说，VAE类似于一个embedding层，以文本数据为例，将其映射到低维空间。由于VAE需要输入一个向量，因此需要对文本进行分词和嵌入/one hot，这样每个token都会得到一个高维度向量，随后将这个高维序列传入编码器（RNN/GRN/CNN/Transformer），来将序列压缩为低维向量，这就是最终需要的低维向量。

在之后的训练过程中，将这个压缩的低维中间向量通过解码器还原为预测的文本序列，并通过loss来控制编码器的嵌入性能。

和Bert类模型的对比

同样作为嵌入模型，VAE和Bert类模型都会将文本通过编码器映射为低维向量，但是两者的训练方式不一样，前者通过重构样本，让模型学文本的原始分布，后者的目标则是通过mask来预测masked token或next token。

由于两者目的不一样，VAE对序列数据和上下文不敏感，只专注还原重构这个任务，Bert则通过自注意力机制，在生成token时会捕捉上下文信息。作为结果，VAE生成的embedding通常表达整体的主题，而不像Bert一样能获取每个词的语义表示。

代码实现

将Chat老师生成了python代码：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader

# 1. 示例文本数据
texts = [
    "hello world",
    "machine learning",
    "deep learning",
    "hello machine",
    "world of learning"
]

# 构建简单词表
vocab = list(set(" ".join(texts).split()))
word2idx = {w: i for i, w in enumerate(vocab)}
idx2word = {i: w for w, i in word2idx.items()}
vocab_size = len(vocab)

# 文本 -> one-hot 向量
def text_to_bow(text):
    vec = torch.zeros(vocab_size)
    for w in text.split():
        vec[word2idx[w]] = 1
    return vec

dataset = torch.stack([text_to_bow(t) for t in texts])

train_loader = DataLoader(dataset, batch_size=2, shuffle=True)

# 2. 文本 VAE 模型
class TextVAE(nn.Module):
    def __init__(self, input_dim, hidden_dim=32, latent_dim=16):
        super().__init__()
        # 编码器
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc_mu = nn.Linear(hidden_dim, latent_dim)
        self.fc_logvar = nn.Linear(hidden_dim, latent_dim)
        # 解码器
        self.fc2 = nn.Linear(latent_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, input_dim)

    def encode(self, x):
        h = F.relu(self.fc1(x))
        return self.fc_mu(h), self.fc_logvar(h)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        h = F.relu(self.fc2(z))
        return torch.sigmoid(self.fc3(h))  # 输出每个词的概率

    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        x_recon = self.decode(z)
        return x_recon, mu, logvar

# 3. 损失函数
def vae_loss(x, x_recon, mu, logvar):
    recon_loss = F.binary_cross_entropy(x_recon, x, reduction='sum')
    kl_loss = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return recon_loss + kl_loss

# 4. 训练
device = "cuda" if torch.cuda.is_available() else "cpu"
model = TextVAE(input_dim=vocab_size).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)

num_epochs = 50
for epoch in range(num_epochs):
    model.train()
    total_loss = 0
    for x in train_loader:
        x = x.to(device)
        optimizer.zero_grad()
        x_recon, mu, logvar = model(x)
        loss = vae_loss(x, x_recon, mu, logvar)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    if (epoch+1) % 10 == 0:
        print(f"Epoch {epoch+1}, Loss: {total_loss/len(dataset):.4f}")

# 5. 生成新文本
model.eval()
with torch.no_grad():
    z = torch.randn(3, 16).to(device)  # 从标准正态采样
    x_gen = model.decode(z).cpu()
    for i, probs in enumerate(x_gen):
        # 输出概率大于0.5的词
        words = [idx2word[j] for j, p in enumerate(probs) if p > 0.5]
        print(f"Generated text {i+1}: {' '.join(words)}")

RQ-VAE（Residual Quantized VAE）

VAE已经将输入的高维embedding降低为了一定程度上的低维embedding，不过要对所有item都保存这个向量，对工业的数据存储压力依旧很大，因此希望对这个输出再进行一次压缩，将连续向量压缩为离散低维向量，这就是RQ-VAE试图解决的问题。这里的RQ指的是向量量化（Vector Quantization, VQ）和残差编码（Residual Encoding）。RQ-VAE试图对Item保存为索引ID，计算时通过ID → 查表 → 点积的方式进行召回。

RQ-VAE的结构

RQ-VAE通过离散码本（Codebook）索引的组合向量来表示原来的VAE embedding。

我对于码本的理解，是对语义嵌入的一次嵌入，只不过这次嵌入的输出是包含语义信息的向量，输入则是语义id（sid）。刚好和文本嵌入相反，文本嵌入输入离散的token，输出连续的embedding，codebook接收带语义信息的embedding，输出语义embedding的语义id。这样不需要直接存embedding，而是通过一个码本就可以解决大规模embedding的存储问题。

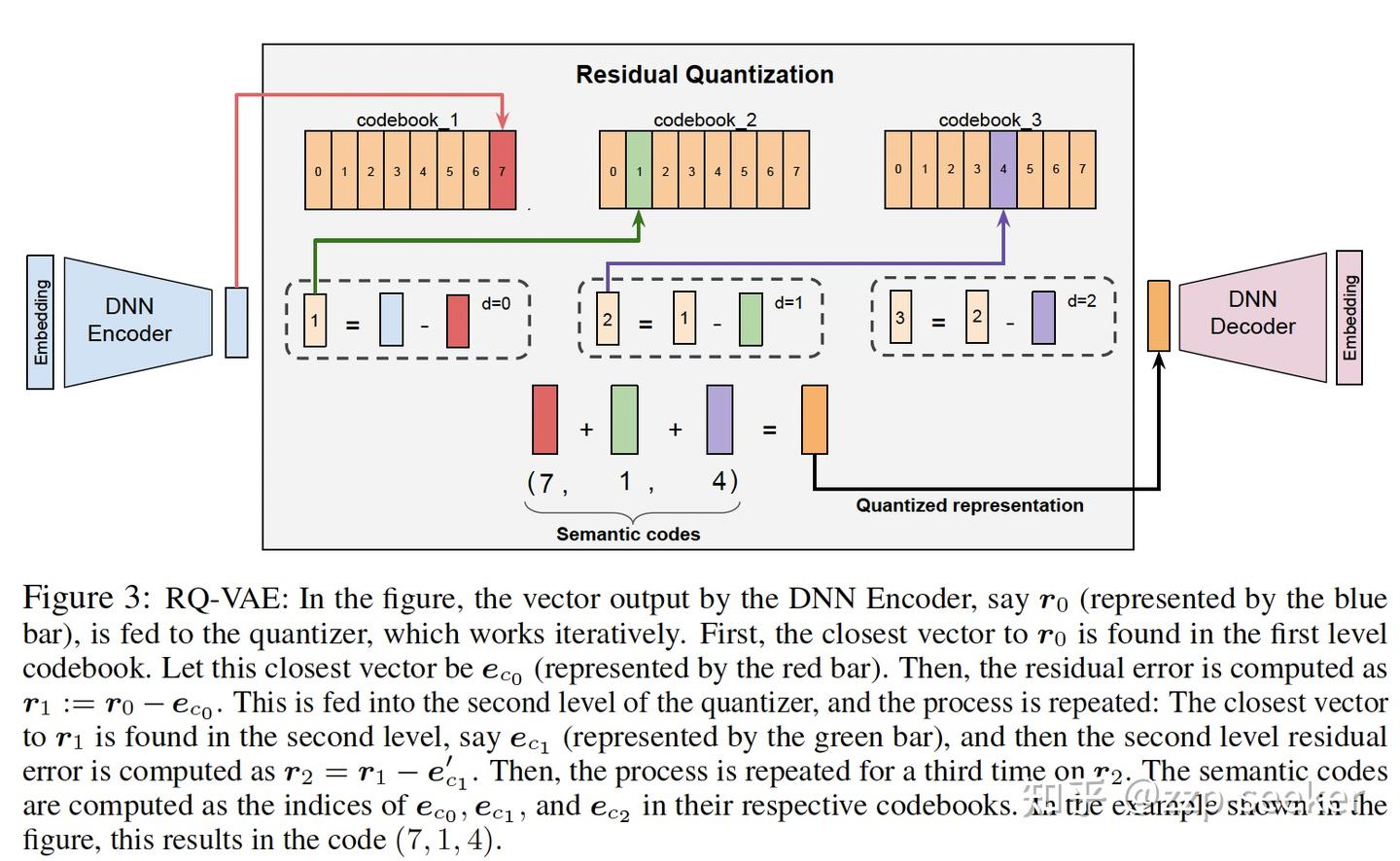
RQ-VAE的结构

在VAE的基础上加了量化和残差的模块，结构如下：

编码器输入数据 $x$，输出潜在向量 $z_e$。
为了引入离散化，RQ-VAE在潜在表示$z_e$上进行残差量化。

初始量化：首先将 $z_e$映射到一个离散的代码簿（Codebook）中。
残差计算：计算初始量化后的残差（Residual），即 $z_e$与其量化表示之间的差异。
残差量化：将残差再次进行量化，并累积到先前的量化结果中。
通过多次残差量化，可以得到一个更精确、更离散的潜在表示。

解码器（Decoder）将量化后的向量 $z_q$ 重构为 $\hat{x}$。

RQ-VAE 的损失函数与 VAE 类似，也有两部分：重构损失保证量化向量重构准确。量化损失（Quantization Loss）保证编码器输出接近码本向量：

$$
\mathcal{L}_{quant} = | \text{sg}[z_e] - z_q |^2 + \beta | z_e - \text{sg}[z_q] |^2
$$

其中 sg 表示 stop-gradient（梯度不反传），用于控制更新方向。

最终损失：
$$
\mathcal{L} = \text{重构损失} + \mathcal{L}_{quant}
$$

下文摘录自知乎

RQ-VAE首先通过编码器E将输入编码成学习到的潜在表示形式在零级（ = 0）处。

在每个级别处，我们有一个码书。然后，通过映射到该级别的最近嵌入来进行量化。最接近的嵌入时的索引表示零级码字。对于下一级 = 1，然后类似于零级，使用第一级的码书计算第一级的代码。这个过程迭代N次，以获得表示语义标识的N个码字元组。这种递归方法近似于从粗到细的粒度对输入进行估计。

为了防止RQ-VAE发生codebook坍塌，即将大部分输入映射到仅几个codebook向量中，我们使用基于k均值聚类的初始codebook初始化。具体而言，在第一个训练批次上应用k均值算法，并使用聚类中心作为初始化，通过聚类特征的指数移动平均值进行更新

码本的更新步骤：一般做法

初始化：首先，通过一些初始方法（如K-means聚类）生成初始码本。

编码（Encoding）：对于每个模型参数（或参数向量），找到与其最接近的码本向量，并计算残差（即原始参数与码本向量之间的差异）。

更新码本（Codebook Update）：
聚合：收集所有映射到同一码本向量的残差。
平均：将这些残差求平均，得到一个新的向量。
更新：用新的向量更新对应的码本向量。

迭代：重复编码和更新步骤，直到码本收敛或达到预设的迭代次数。

RQ-VAE的细节操作，我还不是很理解。Github上有现成的实现代码，还需要debug一下以了解具体是如何实现码本的更新，以及语义对齐，后续如果有更多理解会同步在博客里。

2025/9/14 于苏州

推荐系统

#推荐系统 #生成式推荐 #RQ-VAE

摘录：在大语言模型时代如何改进推荐系统与搜索上一篇

2025Q1-Q3流水账下一篇