这个周末又没啥事,把之前浅尝辄止的多任务学习跟进一下,学习一下PLE。对它进行研究,主要是因为最近在业务上实验了meta的多任务学习框架AdaTT,而在它的官方仓库里刚好实现了多个经典框架。其中PLE网络我看了好几次没看明白,因此花了点时间去研究一下这个经典模型。
多任务,负迁移和跷跷板
PLE(Progressive Layered Extraction)来自于腾讯视频团队2020年发表于RecSys的论文,一举拿下当届RecSys的最佳长论文。论文要解决的问题场景是视频推荐场景。先笼统的介绍论文解决的问题,也就是大部分解读PLE分析文章里不会错过的重点:负迁移问题和跷跷板问题。这两个问题都被认为是一种原因导致的,即多任务之间相关性太低,因此一个任务指标提升会导致另一个任务指标下降,也丧失了多任务中共享参数的意义。
原文中对此举例的是完播率VCR(View Completion Ratio,直接回归预测视频完播率)和有效播放率VTR(View-Through Rate,定义是用户观看某个视频时,是否超过一定时间,二分类任务)。在他们的实验中注意到两个任务出现了翘翘板的现象。
原论文在实验中证明,当时的大部分多任务学习对此的表现都不佳,如果以单任务作为基点,可以看到面对VCR和VTR两个任务,只有MMOE同时超越了两个单任务模型。

我对多任务学习的理解,粗浅认为是为了解决部分任务样本不足的情况,MOE层和Gate层的引入使得其他任务的信息也会通过权重传入不同任务塔。然而跷跷板的现象也是可理解的,比如完播率和播放时长天然就存在一定的负相关,大部分完播率高的视频都是短视频,如果模型输出的都是短视频,显然在视频播放时长这个任务上就会表现不好。
多任务学习一览模型架构
论文给出了多任务学习的框架图,先从左边看,左侧是单层多任务模型,依次为硬参数共享,非对称共享,自定义共享,MMOE和PLE中探索的CGC。
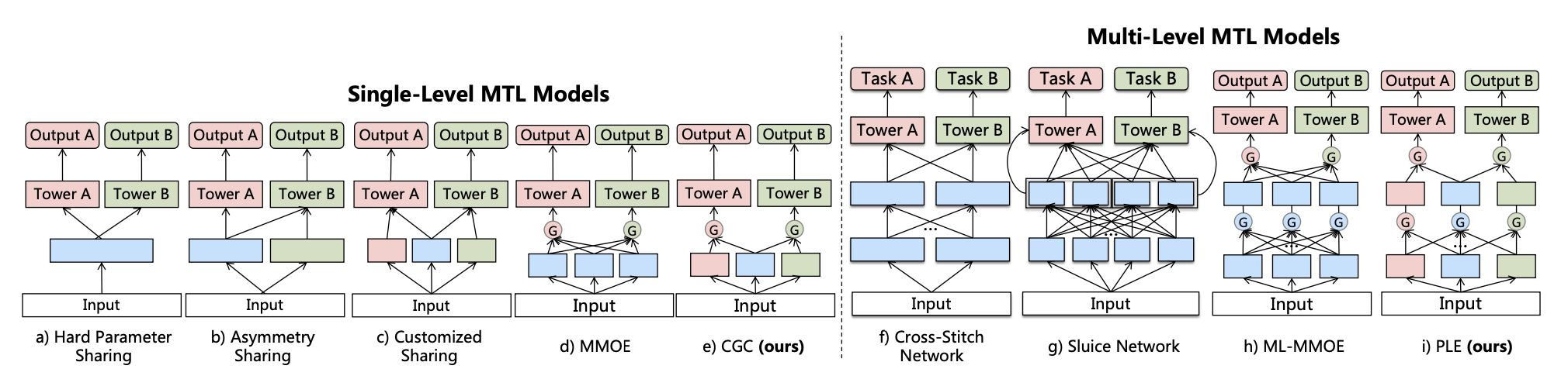
硬参数共享
硬参数共享就是同样的输入,传给不同的任务塔,得到最后的输出。这里给出Meta的实现,非常简炼的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| import torch
import torch.nn as nn
class MLP(nn.Module):
"""
Args:
input_dim (int): 输入维度
mlp_arch (List[int]): mlp不同层神经元数
activation (str):
Call Args:
input (torch.Tensor): tensor of shape (B, I):输入tensor
Returns:
output (torch.Tensor): MLP result
Example::
mlp = MLP(100, [100])
"""
def __init__(
self,
input_dim: int,
mlp_arch: List[int],
activation: str = "RELU",
bias: bool = True,
) -> None:
super().__init__()
mlp_net = []
for mlp_dim in mlp_arch:
mlp_net.append(
nn.Linear(in_features=input_dim, out_features=mlp_dim, bias=bias)
)
if activation == "RELU":
mlp_net.append(nn.ReLU())
else:
raise ValueError("only RELU is included currently")
input_dim = mlp_dim
self.mlp_net = nn.Sequential(*mlp_net)
def forward(
self,
input: torch.Tensor,
) -> torch.Tensor:
return self.mlp_net(input)
class SharedBottom(nn.Module):
def __init__(
self, input_dim: int, hidden_dims: List[int], num_tasks: int, activation: str
) -> None:
super().__init__()
self.bottom_projection = MLP(input_dim, hidden_dims, activation)
self.num_tasks: int = num_tasks
def forward(
self,
input: torch.Tensor,
) -> torch.Tensor:
return self.bottom_projection(input).unsqueeze(1).expand(-1, self.num_tasks, -1)
|
self.bottom_projection(input).unsqueeze(1).expand(-1, self.num_tasks, -1),其中的unsqueeze(1).expand(-1, self.num_tasks, -1)理解为,输入的中间隐藏向量,先是增加了一维空间,然后复制了出 num_tasks 份同样的隐藏向量。
过程为:
1
2
3
| feat = self.bottom_projection(input)
feat = feat.unsqueeze(1)
feat = feat.expand(-1, self.num_tasks, -1)
|
expand只能对已经有的维度修改大小,所以先unsqueeze多一个维度。
非对称共享
看图说话:非对称共享就是两个任务不是都用同样的特征,图里任务A只用了自己的特征,任务B用了全部的特征。这样的话,原有的任务不会被影响,需要增强的任务依旧能获取到需要的额外信息。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class AsymSharedBottom(nn.Module):
def __init__(self, input_dim: int, hidden_dims: List[int], num_tasks: int, activation: str):
super().__init__()
assert num_tasks == 2, "示例只写了2个任务"
self.task1_mlp = MLP(input_dim, hidden_dims, activation)
self.task2_mlp = MLP(input_dim, hidden_dims, activation)
self.num_tasks = num_tasks
self.task2_proj = nn.Linear(hidden_dims[-1]*2, hidden_dims[-1])
def forward(self, x: torch.Tensor):
feat1 = self.task1_mlp(x)
feat2 = self.task2_mlp(x)
feat2 = torch.cat([feat2, feat1.detach()], dim=-1)
feat2 = self.task2_proj(feat2)
out = torch.stack([feat1, feat2], dim=1)
return out
|
自定义共享
自定义共享相当于多了一个可学习的权重网络,为每个任务的特征分配权重,2016年的CrossStitch Net,增加了一个可学习的 cross-stitch 权重矩阵。cross-stitch 权重矩阵的结构如下图:
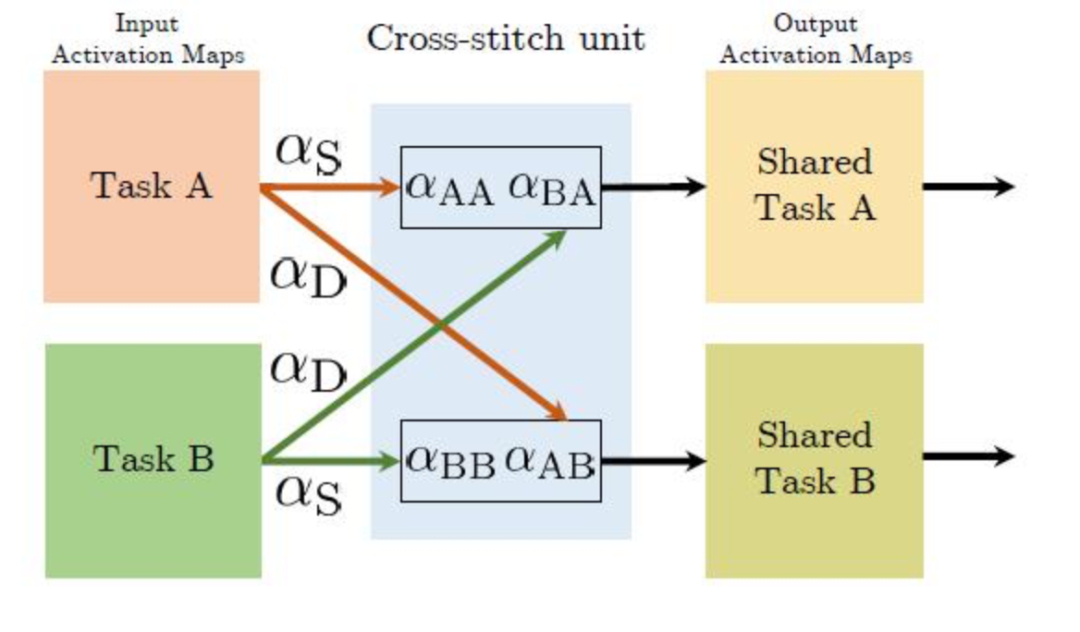
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| class CrossStitch(torch.nn.Module):
"""
cross-stitch
paper title: "Cross-stitch Networks for Multi-task Learning".
paper link: https://openaccess.thecvf.com/content_cvpr_2016/papers/Misra_Cross-Stitch_Networks_for_CVPR_2016_paper.pdf
"""
def __init__(
self,
input_dim: int,
expert_archs: List[List[int]],
num_tasks: int,
activation: str = "RELU",
) -> None:
super().__init__()
self.num_layers: int = len(expert_archs)
self.num_tasks = num_tasks
self.experts = torch.nn.ModuleList()
self.stitchs = torch.nn.ModuleList()
expert_input_dim = input_dim
for layer_ind in range(self.num_layers):
self.experts.append(
torch.nn.ModuleList(
[
MLP(
expert_input_dim,
expert_archs[layer_ind],
activation,
)
for _ in range(self.num_tasks)
]
)
)
self.stitchs.append(
torch.nn.Linear(
self.num_tasks,
self.num_tasks,
bias=False,
)
)
expert_input_dim = expert_archs[layer_ind][-1]
def forward(self, input: torch.Tensor) -> torch.Tensor:
"""
input dim [B, T, D_in]
output dim [B, T, D_out]
"""
x = input
for layer_ind in range(self.num_layers):
expert_out = torch.stack(
[
expert(x[:, expert_ind, :])
for expert_ind, expert in enumerate(self.experts[layer_ind])
],
dim=1,
)
stitch_out = self.stitchs[layer_ind](expert_out.transpose(1, 2)).transpose(
1, 2
)
x = stitch_out
return x
|
CGC
先回顾一下MMOE,MMOE将统一的输入传给不同专家后,多个共享专家提取通用特征,最终输入给每个任务塔的是加权后的专家输出,它假定了每个任务都能用上所有专家的特征的输出。
腾讯团体认为这没有针对每个任务做拆分,不是所有任务都会用上所有的专家输出,如果任务差异大,通用专家效果不好。
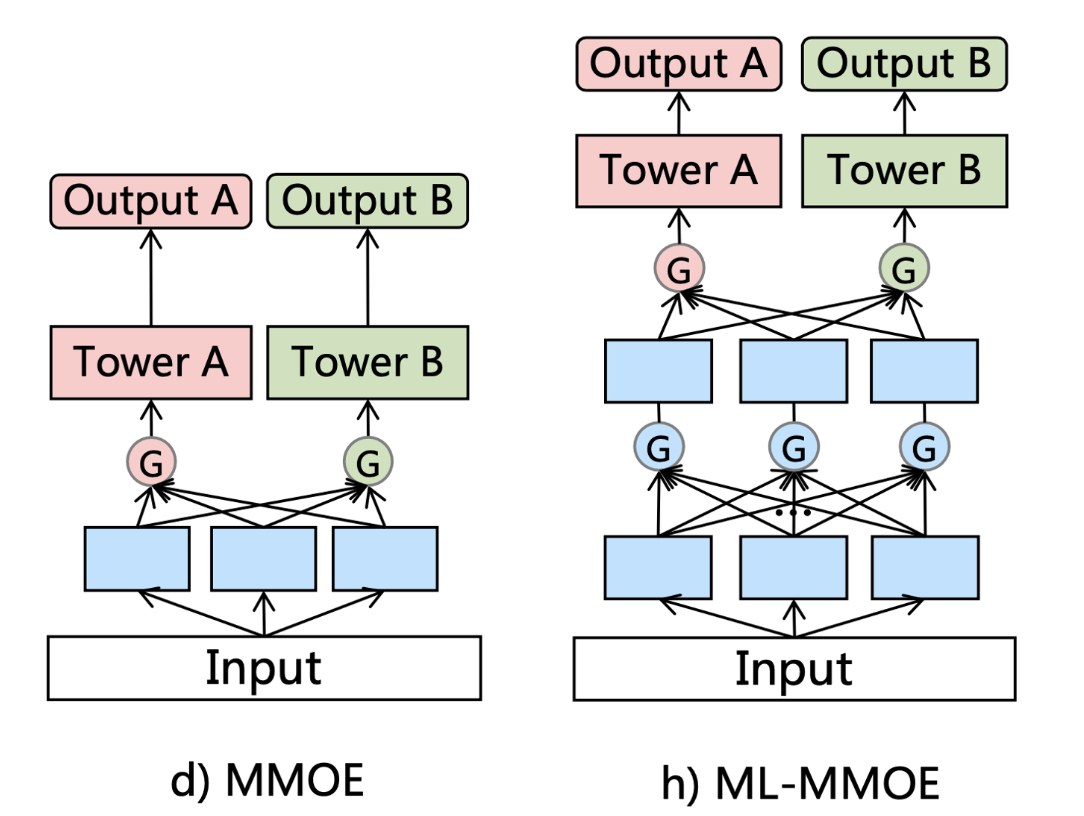
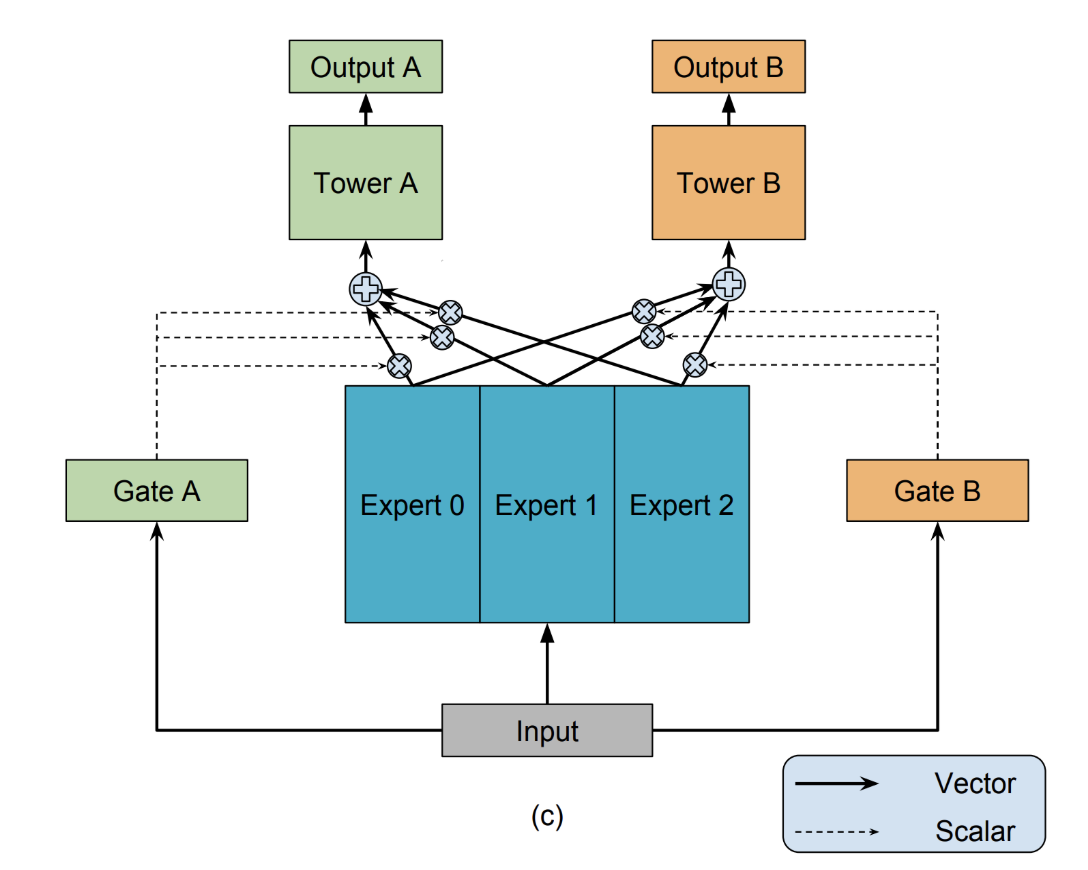
现在来看CGC,CGC是在PLE这篇论文里被同时提出的,也是PLE的基础网络。它更多的是对CrossStitch Net的改进,除了每个任务有独立的专家,门控网络是从具体的任务的专家输出中加权,而是自定义共享里的有选择性的特征共享,而不是像MMOE一样,从共享的专家输出中加权。
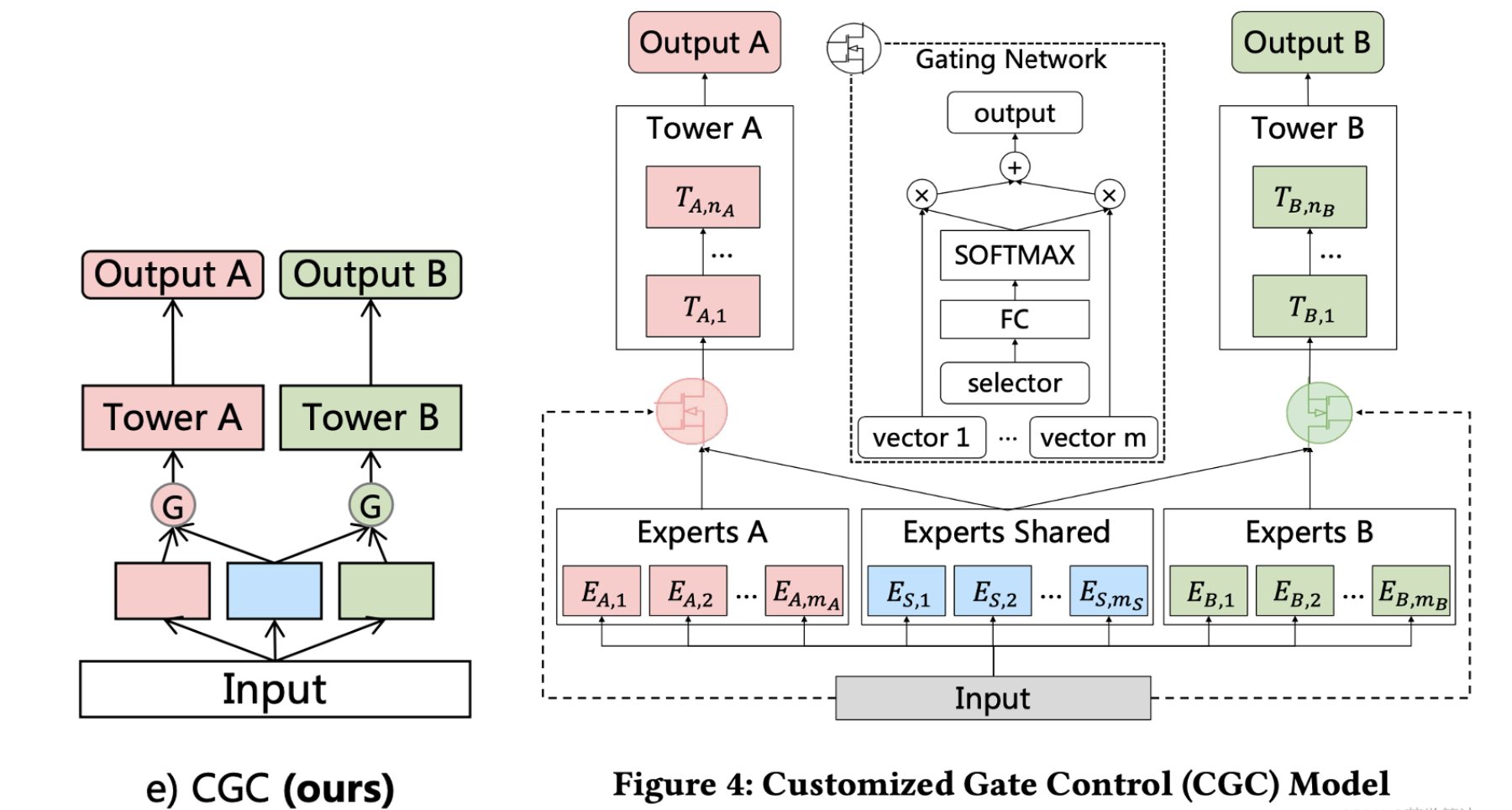
CGC的三个结构:
- 底层网络,就是每个任务的专家网络以及共享网络,他们的输入都是unsqueeze的同样的特征。
- 上层网络,也就是每个任务的任务塔,输出最后每个任务的结果。
- 门控网络,也就是图中白色的网络,通过softmax分配融合特征时的权重配比。
关于这两者的区别,我花了一点时间查询和理解,但是还是感觉理解还是有些欠缺,此处附上GPT老师的回答:
提问:都有门控网络,这不是还是跟mmoe一样加权了吗?
回答:你说得没错,本质上 CGC 也是通过 gate 做加权,但是它和 MMoE 的关键区别在 加权的对象和方式,不是简单把 gate 当作“加权器”。我详细解释下:
1. MMoE 的 gate 加权机制
- MMoE 中,专家是共享的,每个任务有独立 gate。
- 这里的 gate
g_{t,i} 只决定 任务 t 从共享专家 i 获取多少信息。
- 特点:每个专家对所有任务都是一样的输出;gate 只是做“分配”而已。
所以 MMoE 的核心是“共享专家 + 任务特定 gate 分配权重”。
2. CGC 的门控加权机制
- CGC 允许 每个任务有自己的 task-specific 专家,而且每个任务可以选择性地使用 其他任务的专家输出。
- 区别点:
- 加权对象不同:不仅可以加权共享专家,也可以加权其他任务特定专家的输出
- 信息流可以非对称:Task1 可以借 Task2 特征,但 Task2 不一定反向借 Task1
- gate 条件可依赖任务输入:Cross-gating 可以根据输入动态调整共享比例,而不仅是固定专家权重
- 直观理解:MMoE gate 是“专家组合权重”,CGC gate 是“跨任务信息选择权重”。

提问:没有太理解,mmoe加权的是每个专家塔输出的对原始特征的hidden state,cgc加权不也是每个专家塔输出的特征的hidden state吗
回答:你理解得方向没错,本质上都是对专家输出做加权,但是关键区别在 加权对象和加权的粒度/信息流方式

PLE是对CGC的改进版本,因此此处未附上CGC的实现代码。
PLE
PLE把CGC做深了,观察下图的Multi-level Extraction Networks,是多个专家的堆叠,是作者认为在前期,加深专家网络能够提取到更深层的语义信息。在每一层,共享专家不断吸收各自任务专家之间的信息,而任务独有的专家则从共享专家中吸收有用的信息。
在多个网络提取特征之后,才将特征传入CGC网络,这种方式被作者称为是渐进式的特征提取,这也是PLE的名字由来:Progressive Layered Extraction。

附上代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
| class PLE(nn.Module):
"""
PLE 明确区分 共享专家(shared experts) 和 任务专属专家(task-specific experts),并采用 逐层提取机制(progressive routing mechanism),逐步提取和分离更深层的语义知识。
当只有 一层提取层 时,PLE 会退化为 CGC 网络。
⸻
参数说明
• input_dim:输入 embedding 的维度
• expert_out_dims(List[List[int]]):每层专家输出的维度列表。列表长度 = 提取层数,每个子列表表示该层每个专家的输出维度
• num_tasks:任务数量
• num_task_experts:每个任务模块在每层的专家数量
• 如果所有任务的专家数量相同,用整数表示
• 如果不同任务专家数量不同,用整数列表表示
• num_shared_experts:每层共享模块的专家数量
⸻
调用参数
• inputs:输入 tensor,维度为 [batch_size, num_tasks + 1, input_dim]
• 前 num_tasks 个元素为任务专属模块的输入
• 最后一个元素为共享模块的输入
• 同一模块中的所有专家共享同一个输入
⸻
返回值
• output:提取层的输出,用于输入到任务专属塔网络(task-specific tower networks)
• 输出是 一个列表,列表中每个元素对应一个任务的输出 tensor
Example::
PLE(
input_dim=256,
expert_out_dims=[[128]],
num_tasks=8,
num_task_experts=2,
num_shared_experts=2,
)
"""
def __init__(
self, input_dim: int, expert_out_dims: List[List[int]],
num_tasks: int, num_task_experts: Union[int, List[int]], num_shared_experts: int,
activation: str = "RELU",
) -> None:
super().__init__()
if len(expert_out_dims) == 0:
raise ValueError("Expert out dims cannot be empty list")
self.num_extraction_layers: int = len(expert_out_dims)
self.num_tasks = num_tasks
self.num_task_experts = num_task_experts
if type(num_task_experts) is int:
self.total_experts_per_layer: int = (
num_task_experts * num_tasks + num_shared_experts
)
else:
self.total_experts_per_layer: int = (
sum(num_task_experts) + num_shared_experts
)
assert len(num_task_experts) == num_tasks
self.num_shared_experts = num_shared_experts
self.experts = nn.ModuleList()
expert_input_dim = input_dim
for expert_out_dim in expert_out_dims:
self.experts.append(
nn.ModuleList(
[MLP(expert_input_dim, expert_out_dim, activation) for i in range(self.total_experts_per_layer) ])
)
expert_input_dim = expert_out_dim[-1]
self.gate_weights = nn.ModuleList()
selector_dim = input_dim
for i in range(self.num_extraction_layers):
expert_out_dim = expert_out_dims[i]
if type(num_task_experts) is int:
gate_weights_in_layer = nn.ModuleList(
[
nn.Sequential(
nn.Linear(
selector_dim, num_task_experts + num_shared_experts
),
nn.Softmax(dim=-1),
)
for i in range(num_tasks)
]
)
else:
gate_weights_in_layer = nn.ModuleList(
[
nn.Sequential(nn.Linear(selector_dim, num_task_experts[i] + num_shared_experts),nn.Softmax(dim=-1),)for i in range(num_tasks)])
if i != self.num_extraction_layers - 1:
gate_weights_in_layer.append(
nn.Sequential(
nn.Linear(selector_dim, self.total_experts_per_layer),
nn.Softmax(dim=-1),
)
)
self.gate_weights.append(gate_weights_in_layer)
selector_dim = expert_out_dim[-1]
if type(self.num_task_experts) is list:
experts_idx_2_task_idx = []
for i in range(num_tasks):
experts_idx_2_task_idx += [i] * self.num_task_experts[i]
experts_idx_2_task_idx += [num_tasks] * num_shared_experts
self.experts_idx_2_task_idx: List[int] = experts_idx_2_task_idx
def forward(
self,
inputs: torch.Tensor,
) -> torch.Tensor:
for layer_i in range(self.num_extraction_layers):
if type(self.num_task_experts) is int:
experts_out = torch.stack(
[
self.experts[layer_i][expert_i](
inputs[
:,
min(expert_i // self.num_task_experts, self.num_tasks),
:,
]
)
for expert_i in range(self.total_experts_per_layer)
],
dim=1,
)
else:
experts_out = torch.stack(
[
self.experts[layer_i][expert_i](
inputs[
:,
self.experts_idx_2_task_idx[expert_i],
:,
]
)
for expert_i in range(self.total_experts_per_layer)
],
dim=1,
)
gates_out = []
prev_idx = 0
for gate_i in range(len(self.gate_weights[layer_i])):
if gate_i == self.num_tasks:
selected_matrix = experts_out
else:
if type(self.num_task_experts) is int:
task_experts_out = experts_out[
:,
(gate_i * self.num_task_experts) : (gate_i + 1)
* self.num_task_experts,
:,
]
else:
next_idx = prev_idx + self.num_task_experts[gate_i]
task_experts_out = experts_out[
:,
prev_idx:next_idx,
:,
]
prev_idx = next_idx
shared_experts_out = experts_out[
:,
-self.num_shared_experts :,
:,
]
selected_matrix = torch.concat(
[task_experts_out, shared_experts_out], dim=1
)
gates_out.append(
torch.bmm(
self.gate_weights[layer_i][gate_i](
inputs[:, gate_i, :]
).unsqueeze(dim=1),
selected_matrix,
)
)
inputs = torch.cat(gates_out, dim=1)
return inputs
|
逻辑都一行行debug写在注释里了,真的燃尽了。Meta的工程师不知道是不是有压行的习惯,加上我pytorch功底不到位,看着比较吃力。
损失函数的改进
对比起模型层面的改进,论文对损失函数的改进很有业务价值。传统的多任务模型采用的是子任务的加权损失,但是在部分业务场景下有问题,如果用户行为标签是有序的,也就是子任务是一个递进的序列关系,例如用户只有点击了才会有后续的标签,因此存在样本空间不一致的情况。
论文对此的解决方案是在计算每个任务损失的时候忽略不在当前空间的样本,即不同任务以及使用自己的样本,但是使用的权重是整个模型的权重。
其次,对于子任务的权重,之前是人工设定,论文中改为动态调整的方式,首先对第$k$个子任务设置一个初始值,之后每一步根据跟新率更新其损失权重。
2025/9/20 于苏州


![]()





