多任务学习：通过Grad Norm调整多loss权重

最近在持续更新自己的开源推荐算法框架NextRec，目前已经更新到0.4.11，初期的大部分里程碑都进行的差不多了。

在开发过程中，对个人最有收获的，无疑是对不少推荐算法的细节（尤其是工程问题，分布式训练等等）都有了一些更深的体验和了解，很多问题都曾是令前辈们头疼的难题，但是现在都有了更好的解决方案。这次要学习的主题就是，在多任务模型中，逃不过的一个难题：如何平衡多任务的loss。

我们在业务中尝试多任务学习的时间并不长，频繁接触也只是近半年的事。在业务中，我们大多还是以手动拍脑袋决定不同任务的loss weight，觉得哪个任务重要，我们就给更高的权重。在我们的场景下，包含点击，注册，转化等多个任务，对于业务场景，无疑更关心最后的转化任务。因此，我们通常会给最后一个任务赋予最高的权重。

在NextRec里，我们通过对模型进行compile时，手动赋予不同任务的权重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from nextrec.models.multi_task.esmm import ESMM
from nextrec.basic.features import DenseFeature, SparseFeature, SequenceFeature

model = ESMM(
    dense_features=dense_features,
    sparse_features=sparse_features,
    sequence_features=sequence_features,
    ctr_params={"dims": [64, 32], "activation": "relu", "dropout": 0.4},
    cvr_params={"dims": [64, 32], "activation": "relu", "dropout": 0.4},
    target=task_labels,
    task=["click", "conversion"],
)

model.compile(
    optimizer="adam",
    optimizer_params={"lr": 5e-4, "weight_decay": 1e-4},
    loss=["bce", "bce"],
    loss_weights=[0.3, 0.7] # 我们在这里赋予任务权重
)

在每个epoch里，会为每个任务的loss乘以这个权重值。

1
2
3
4
5
6
7
8
9
10
class BaseModel:
		...
    def compute_loss(self, y_pred, y_true):
    		...
        if isinstance(self.loss_weights, (list, tuple)):
            task_losses = [
                task_loss * self.loss_weights[i]
                for i, task_loss in enumerate(task_losses)
            ]
        return torch.stack(task_losses).sum()

这是一个非常粗浅的，基于先验知识的方法，显然并不符合数据驱动的宗旨。这当中有几个核心问题：

  1. 不同任务的loss的尺度是不一样的，尤其是出现在回归任务和分类任务时，mse和bce的尺度差很大，导致大的loss会主导整个训练任务。对于这个问题，工业界层用loss归一化来调整。
  2. 不同任务的loss收敛速度不一致，对于简单的任务，loss很快收敛，而难的任务则收敛的很慢。然而全局而言，模型只看到了整体的loss快速收敛，而忽视了困难任务。

在实际场景下，不同任务的损失权重，应该随着样本的变化，训练的变化，才能找到最佳的数值。对于这个问题，2018年发布的论文GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks中给出了作者的解决方案。

GradNorm

GradNorm的主要思想是，通过每个任务对共享参数的梯度强度，来更细致的了解哪个任务对参数的影响更大，进而调整弱势任务的权重。这比loss更近了一步，上升到了参数层面。

我们先找到多任务模型的共享参数层$W$，找到它的梯度$$G_i = \left| \nabla_W \big( w_i \mathcal{L}_i \big) \right|$$。

为什么是共享层梯度？因为任务塔的梯度是互相不影响的，大家竞争的点只是共享层。

GradNorm定义目标梯度是$$\tilde{G}_i = \bar{G} \cdot \left( \frac{\mathcal{L}_i(t)}{\mathcal{L}_i(0)} \right)^{\alpha}$$。其中$\bar{G}$是所有任务当前梯度的平均，后者则是任务$i$的相对训练进度。

所有任务当前梯度的平均是指：对于每个任务i，先看它在共享参数上的梯度，乘当前权重，然后取梯度的l2正则，最后给所有任务做平均。这就得到了等号右边的第一项。

在第二项，任务$i$的相对训练进度里，分子是任务$i$当前时刻的损失，分母则是起始时刻的损失。它的含义是当前时刻，任务的loss相比刚开始减少的比例，由于无量纲，它更能反映当前任务的学习速度。

在得到这个学习速度以后，通过一个$\alpha$参数来控制梯度的权重占比。可以预见的是，学的越快，第二项越小，整体梯度也越小。

最后在每个迭代时，先计算各任务loss，计算加权总loss，更新模型参数；随后计算每个任务的共享层梯度参数，并构造出加权后的新梯度，最后最小化GradNorm的loss，来更新权重。

代码实现

在NextRec 0.4.13版本中，加入了对grad norm的支持，只需要将之前comile里的loss_weights方法改为{"method": "grad_norm", "alpha": 1.5, "lr": 0.025}或”grad_norm”即可。

1
2
3
4
5
6
model.compile(
    optimizer="adam",
    optimizer_params={"lr": 5e-4, "weight_decay": 1e-4},
    loss=["bce", "bce"],
    loss_weights={"method": "grad_norm", "alpha": 1.5, "lr": 0.025}, # 或者可以直接写"grad_norm"
)

我们来看下底层实现，核心代码位于nextrec.loss.grad_norm.py。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
def get_grad_norm_shared_params(
    model: torch.nn.Module,
    shared_modules: Iterable[str] | None = None,
) -> list[torch.nn.Parameter]:
  	"""
  	获取共享层参数的工具函数
  	"""
    if not shared_modules:
        return [p for p in model.parameters() if p.requires_grad]
    shared_params = []
    seen = set()
    for name in shared_modules:
        module = getattr(model, name, None)
        if module is None:
            continue
        for param in module.parameters():
            if param.requires_grad and id(param) not in seen:
                shared_params.append(param)
                seen.add(id(param))
    if not shared_params:
        return [p for p in model.parameters() if p.requires_grad]
    return shared_params
  
class GradNormLossWeighting:
    """
    Adaptive multi-task loss weighting with GradNorm.

    Args:
        num_tasks (int):
            任务数量，必须大于 1。

        alpha (float):
            GradNorm 的平衡强度系数，用于控制“扶弱抑强”的程度。
            alpha 越大，学习进度较慢的任务将获得更大的梯度权重。
            论文中常用取值为 1.5。

        lr (float):
            用于优化任务权重 w_i 的学习率。
            注意该学习率只作用于权重参数，不影响模型参数。

        init_weights (Iterable[float] | None):
            各任务的初始损失权重。
            若为 None，则所有任务初始权重均设为 1。

        device (torch.device | str | None):
            权重参数所在的设备（CPU / GPU）。
            若为 None，则使用默认设备。

        ema_decay (float | None):
            可选的 EMA（指数滑动平均）衰减系数，用于平滑各任务的
            当前 loss，从而稳定相对训练进度的计算。
            取值范围为 [0.0, 1.0)，值越大，平滑程度越高。
            若为 None，则直接使用当前 batch 的 loss。

        init_ema_steps (int):
            用于构建初始 loss 基准的 EMA 累积步数。
            当该值大于 0 时，将在前 init_ema_steps 个 step 内
            使用 EMA 累积 loss，并在完成后冻结为初始 loss，
            以避免仅用首个 batch 作为基准带来的不稳定性。

        init_ema_decay (float):
            在构建初始 loss EMA（init_ema_steps > 0）时使用的
            EMA 衰减系数。通常可取 0.9 ~ 0.99。

        eps (float):
            数值稳定性用的小常数，用于避免除零或梯度范数为 0 的情况。
    """

    def __init__(
        self,
        num_tasks: int,
        alpha: float = 1.5,
        lr: float = 0.025,
        init_weights: Iterable[float] | None = None,
        device: torch.device | str | None = None,
        ema_decay: float | None = None,
        init_ema_steps: int = 0,
        init_ema_decay: float = 0.9,
        eps: float = 1e-8,
    ) -> None:
        if num_tasks <= 1:
            raise ValueError("GradNorm requires num_tasks > 1.")
        self.num_tasks = int(num_tasks)
        self.alpha = float(alpha)
        self.eps = float(eps)
        if ema_decay is not None:
            ema_decay = float(ema_decay)
            if ema_decay < 0.0 or ema_decay >= 1.0:
                raise ValueError("ema_decay must be in [0.0, 1.0).")
        self.ema_decay = ema_decay
        self.init_ema_steps = int(init_ema_steps)
        if self.init_ema_steps < 0:
            raise ValueError("init_ema_steps must be >= 0.")
        self.init_ema_decay = float(init_ema_decay)
        if self.init_ema_decay < 0.0 or self.init_ema_decay >= 1.0:
            raise ValueError("init_ema_decay must be in [0.0, 1.0).")
        self.init_ema_count = 0

        if init_weights is None:
            weights = torch.ones(self.num_tasks, dtype=torch.float32)
        else:
            weights = torch.tensor(list(init_weights), dtype=torch.float32)
            if weights.numel() != self.num_tasks:
                raise ValueError(
                    "init_weights length must match num_tasks for GradNorm."
                )
        if device is not None:
            weights = weights.to(device)
        self.weights = nn.Parameter(weights)
        self.optimizer = torch.optim.Adam([self.weights], lr=float(lr))

        self.initial_losses: torch.Tensor | None = None
        self.initial_losses_ema: torch.Tensor | None = None
        self.loss_ema: torch.Tensor | None = None
        self.pending_grad: torch.Tensor | None = None

    def to(self, device):
        device = torch.device(device)
        self.weights.data = self.weights.data.to(device)
        if self.initial_losses is not None:
            self.initial_losses = self.initial_losses.to(device)
        if self.initial_losses_ema is not None:
            self.initial_losses_ema = self.initial_losses_ema.to(device)
        if self.loss_ema is not None:
            self.loss_ema = self.loss_ema.to(device)
        return self

    def compute_weighted_loss(
        self, 
        task_losses: list[torch.Tensor],
        shared_params: Iterable[torch.nn.Parameter],
    ) -> torch.Tensor:
        """
        计算整体的损失并加权梯度损失
        """
        if len(task_losses) != self.num_tasks:
            raise ValueError(
                f"Expected {self.num_tasks} task losses, got {len(task_losses)}."
            )
        # 先找到所有的共享层参数
        shared_params = [p for p in shared_params if p.requires_grad]
        if not shared_params:
            return torch.stack(task_losses).sum()

        with torch.no_grad():
            loss_values = torch.tensor(
                [loss.item() for loss in task_losses], device=self.weights.device
            )
            # 这里的逻辑是用前几个step的ema loss来代替初始的loss，这样数值更稳定
            if self.initial_losses is None:
                if self.init_ema_steps > 0:
                    if self.initial_losses_ema is None:
                        self.initial_losses_ema = loss_values
                    else:
                        self.initial_losses_ema = (
                            self.init_ema_decay * self.initial_losses_ema
                            + (1.0 - self.init_ema_decay) * loss_values
                        )
                    self.init_ema_count += 1
                    if self.init_ema_count >= self.init_ema_steps:
                        self.initial_losses = self.initial_losses_ema.clone()
                else:
                    self.initial_losses = loss_values
				# 用当前的权重，得到一个当前的多任务损失
        weights_detached = self.weights.detach()
        weighted_losses = [
            weights_detached[i] * task_losses[i] for i in range(self.num_tasks)
        ]
        total_loss = torch.stack(weighted_losses).sum()
				# 计算得到共享层的梯度
        grad_norms = self.compute_grad_norms(task_losses, shared_params)
        with torch.no_grad():
            if self.ema_decay is not None:
                if self.loss_ema is None:
                    self.loss_ema = loss_values
                else:
                    self.loss_ema = (
                        self.ema_decay * self.loss_ema
                        + (1.0 - self.ema_decay) * loss_values
                    )
                ratio_source = self.loss_ema
            else:
                ratio_source = loss_values
            if self.initial_losses is not None:
                base_initial = self.initial_losses
            elif self.initial_losses_ema is not None:
                base_initial = self.initial_losses_ema
            else:
                base_initial = loss_values
            loss_ratios = ratio_source / (base_initial + self.eps)
            inv_rate = loss_ratios / (loss_ratios.mean() + self.eps)
            target = grad_norms.mean() * (inv_rate**self.alpha)

        grad_norm_loss = F.l1_loss(grad_norms, target.detach(), reduction="sum")
        grad_w = torch.autograd.grad(grad_norm_loss, self.weights, retain_graph=True)[0]
        self.pending_grad = grad_w.detach()

        return total_loss

    def compute_grad_norms(self, task_losses, shared_params):
        grad_norms = []
        # 对每个任务的loss求共享参数的梯度
        # 最终返回每个任务的梯度范数
        for i, task_loss in enumerate(task_losses):
            grads = torch.autograd.grad(
                self.weights[i] * task_loss,
                shared_params,
                retain_graph=True,
                create_graph=True,
                allow_unused=True,
            )

            sq_sum = torch.zeros((), device=self.weights.device)
            any_used = False
            for g in grads:
                if g is not None:
                    any_used = True
                    sq_sum = sq_sum + g.pow(2).sum()

            if not any_used:
                total_norm = torch.tensor(self.eps, device=self.weights.device)
            else:
                total_norm = torch.sqrt(sq_sum + self.eps)

            grad_norms.append(total_norm)

        return torch.stack(grad_norms)
		
    # 梯度截断和归一化
    def step(self) -> None:
        if self.pending_grad is None:
            return

        self.optimizer.zero_grad(set_to_none=True)

        if self.weights.grad is None:
            self.weights.grad = torch.zeros_like(self.weights)
        self.weights.grad.copy_(self.pending_grad)

        self.optimizer.step()

        with torch.no_grad():
            w = self.weights.clamp(min=self.eps)
            w = w * self.num_tasks / (w.sum() + self.eps)
            self.weights.copy_(w)

        self.pending_grad = None

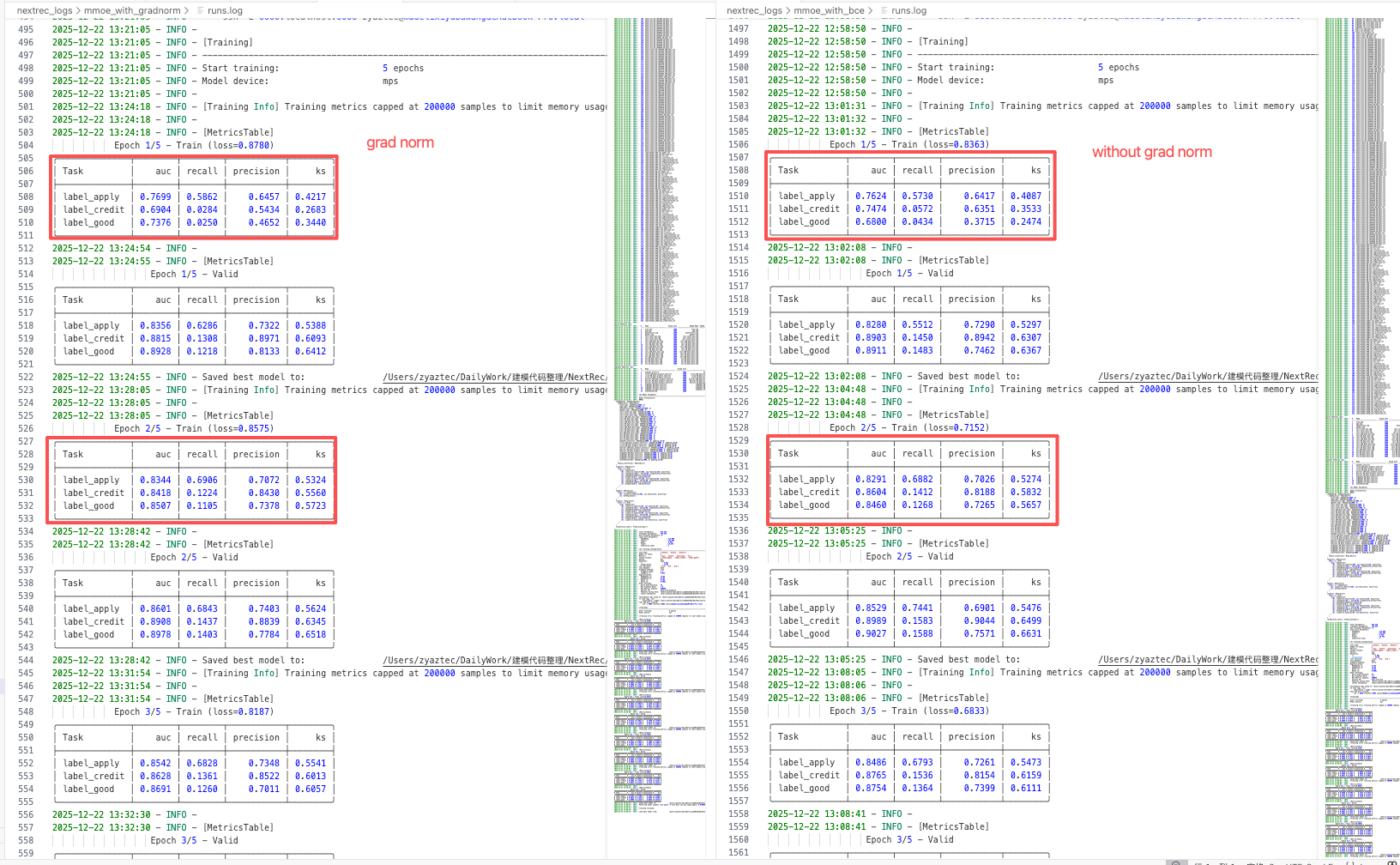
离线指标

在业务上的离线数据集上进行了消融实验，量级为30万+，训练任务分别是是否响应，是否转化，是否优质客户。其中后两项任务的样本量级较少，存在分布不平衡。

我们使用MMOE作为baseline模型，bce作为损失函数，分别采用grad norm和不采用grad norm训练，结果如下。

251222-1

可以注意到，使用grad norm以后，原本样本数量相对较少的难分任务label_good拥有了更高的auc，说明grad norm一定程度上更重视这个任务的梯度，帮助了该任务更好的收敛。

2025/12/21 于苏州